Premier Rock Forum

Rotten Tanx wrote:Without lamps there'd be no light.

Herr Tim wrote:It would be a vast understatement to say that numbers are important.

Andrew L. wrote:Trivia question: When did the number zero first enter western/European mathematics?

Andrew L. wrote:Trivia question: When did the number zero first enter western/European mathematics?

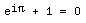
robert thefamilyghost wrote:

Andrew L. wrote:Trivia question: When did the number zero first enter western/European mathematics?

i had to look it up, but in 1202 when Fibonacci published Liber Abaci in which he introduced arabic numerals to europe...and though it was not the first western book to do so, it was aimed at merchants and such to demonstrate how this number system was far more practical and efficient in bookkeeping and all other financial calculations than the roman numeral system...thus the ideas actually gained more mass appeal and helped the public to accept this as a number system...

A symbol for what is not there, an emptiness that increases any number it's added to, an inexhaustible and indispensable paradox. As we enter the year 2000, zero is once again making its presence felt. Nothing itself, it makes possible a myriad of calculations. Indeed, without zero mathematics as we know it would not exist. And without mathematics our understanding of the universe would be vastly impoverished. But where did this nothing, this hollow circle, come from? Who created it? And what, exactly, does it mean?

Robert Kaplan's The Nothing That Is: A Natural History of Zero begins as a mystery story, taking us back to Sumerian times, and then to Greece and India, piecing together the way the idea of a symbol for nothing evolved. Kaplan shows us just how handicapped our ancestors were in trying to figure large sums without the aid of the zero. (Try multiplying CLXIV by XXIV). Remarkably, even the Greeks, mathematically brilliant as they were, didn't have a zero--or did they? We follow the trail to the East where, a millennium or two ago, Indian mathematicians took another crucial step. By treating zero for the first time like any other number, instead of a unique symbol, they allowed huge new leaps forward in computation, and also in our understanding of how mathematics itself works.

In the Middle Ages, this mathematical knowledge swept across western Europe via Arab traders. At first it was called "dangerous Saracen magic" and considered the Devil's work, but it wasn't long before merchants and bankers saw how handy this magic was, and used it to develop tools like double-entry bookkeeping. Zero quickly became an essential part of increasingly sophisticated equations, and with the invention of calculus, one could say it was a linchpin of the scientific revolution. And now even deeper layers of this thing that is nothing are coming to light: our computers speak only in zeros and ones, and modern mathematics shows that zero alone can be made to generate everything.

Robert Kaplan serves up all this history with immense zest and humor; his writing is full of anecdotes and asides, and quotations from Shakespeare to Wallace Stevens extend the book's context far beyond the scope of scientific specialists. For Kaplan, the history of zero is a lens for looking not only into the evolution of mathematics but into very nature of human thought. He points out how the history of mathematics is a process of recursive abstraction: how once a symbol is created to represent an idea, that symbol itself gives rise to new operations that in turn lead to new ideas. The beauty of mathematics is that even though we invent it, we seem to be discovering something that already exists.

The joy of that discovery shines from Kaplan's pages, as he ranges from Archimedes to Einstein, making fascinating connections between mathematical insights from every age and culture. A tour de force of science history, The Nothing That Is takes us through the hollow circle that leads to infinity.